Hendrik/xgboost
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

Correcting small typos in documentation. (#1901)

Browse Source
This commit is contained in:
Kyle Willett 2016-12-31 04:47:51 -08:00 committed by Tianqi Chen
parent f5c85836bf
commit 7e07b2b93d
5 changed files with 58 additions and 58 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

38
doc/model.md
View File

@ -53,11 +53,11 @@ Which solution among the three do you think is the best fit?
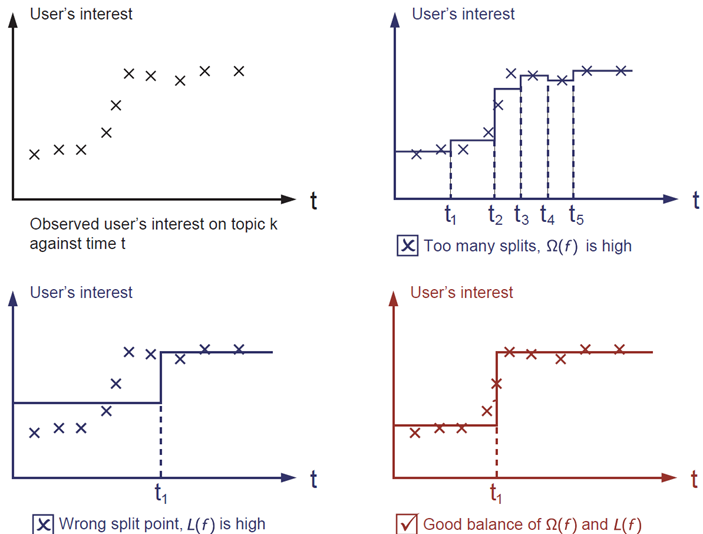
![Step function](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/step_fit.png)
The answer is already marked as red. Please think if it is reasonable to you visually. The general principle is we want a ***simple*** and ***predictive*** model.
The correct answer is marked in red. Please consider if this visually seems a reasonable fit to you. The general principle is we want both a ***simple*** and ***predictive*** model.
The tradeoff between the two is also referred as bias-variance tradeoff in machine learning.
### Why introduce the general principle
### Why introduce the general principle?
The elements introduced above form the basic elements of supervised learning, and they are naturally the building blocks of machine learning toolkits.
For example, you should be able to describe the differences and commonalities between boosted trees and random forests.
Understanding the process in a formalized way also helps us to understand the objective that we are learning and the reason behind the heuristics such as
@ -72,17 +72,17 @@ that classifies whether someone will like computer games.
![CART](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/cart.png)
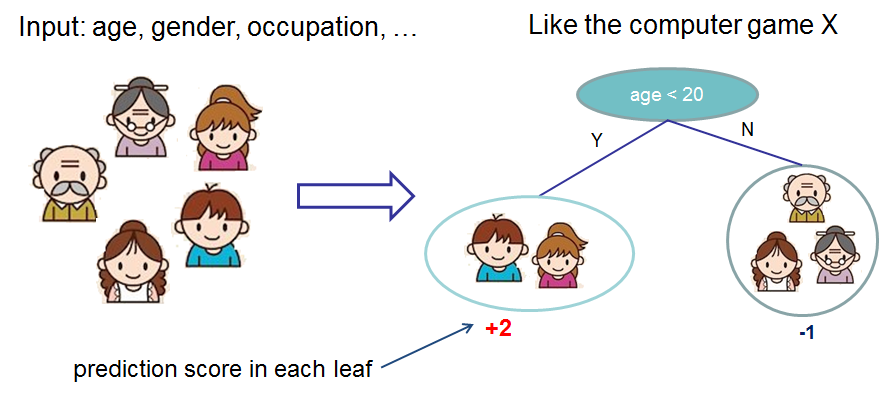
We classify the members of a family into different leaves, and assign them the score on corresponding leaf.
We classify the members of a family into different leaves, and assign them the score on the corresponding leaf.
A CART is a bit different from decision trees, where the leaf only contains decision values. In CART, a real score
is associated with each of the leaves, which gives us richer interpretations that go beyond classification.
This also makes the unified optimization step easier, as we will see in later part of this tutorial.
This also makes the unified optimization step easier, as we will see in a later part of this tutorial.
Usually, a single tree is not strong enough to be used in practice. What is actually used is the so-called
tree ensemble model, that sums the prediction of multiple trees together.
tree ensemble model, which sums the prediction of multiple trees together.
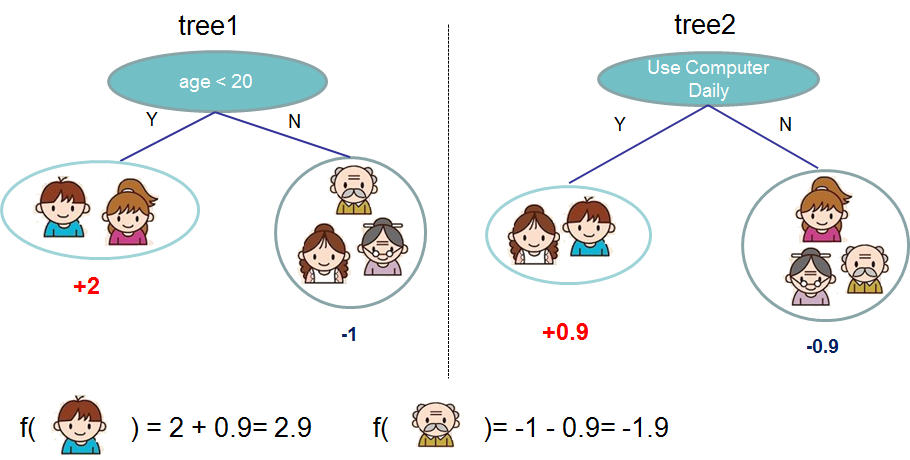
![TwoCART](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/twocart.png)
Here is an example of tree ensemble of two trees. The prediction scores of each individual tree are summed up to get the final score.
Here is an example of a tree ensemble of two trees. The prediction scores of each individual tree are summed up to get the final score.
If you look at the example, an important fact is that the two trees try to *complement* each other.
Mathematically, we can write our model in the form
@ -97,26 +97,26 @@ where ``$ K $`` is the number of trees, ``$ f $`` is a function in the functiona
```
Now here comes the question, what is the *model* for random forests? It is exactly tree ensembles! So random forests and boosted trees are not different in terms of model,
the difference is how we train them. This means if you write a predictive service of tree ensembles, you only need to write one of them and they should directly work
for both random forests and boosted trees. One example of why elements of supervised learning rocks.
for both random forests and boosted trees. One example of why elements of supervised learning rock.
Tree Boosting
-------------
After introducing the model, let us begin with the real training part. How should we learn the trees?
The answer is, as is always for all supervised learning models: *define an objective function, and optimize it*!
Assume we have the following objective function (remember it always need to contain training loss, and regularization)
Assume we have the following objective function (remember it always needs to contain training loss and regularization)
```math
\text{obj} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) \\
```
### Additive Training
First thing we want to ask is what are the ***parameters*** of trees.
You can find what we need to learn are those functions ``$f_i$``, with each containing the structure
First thing we want to ask is what are the ***parameters*** of trees?
You can find that what we need to learn are those functions ``$f_i$``, with each containing the structure
of the tree and the leaf scores. This is much harder than traditional optimization problem where you can take the gradient and go.
It is not easy to train all the trees at once.
Instead, we use an additive strategy: fix what we have learned, add one new tree at a time.
We note the prediction value at step ``$t$`` by ``$ \hat{y}_i^{(t)}$``, so we have
Instead, we use an additive strategy: fix what we have learned, and add one new tree at a time.
We write the prediction value at step ``$t$`` as ``$ \hat{y}_i^{(t)}$``, so we have
```math
\hat{y}_i^{(0)} &= 0\\
@ -140,7 +140,7 @@ If we consider using MSE as our loss function, it becomes the following form.
& = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + constant
```
The form of MSE is friendly, with a first order term (usually called residual) and a quadratic term.
The form of MSE is friendly, with a first order term (usually called the residual) and a quadratic term.
For other losses of interest (for example, logistic loss), it is not so easy to get such a nice form.
So in the general case, we take the Taylor expansion of the loss function up to the second order
@ -162,18 +162,18 @@ After we remove all the constants, the specific objective at step ``$t$`` become
This becomes our optimization goal for the new tree. One important advantage of this definition is that
it only depends on ``$g_i$`` and ``$h_i$``. This is how xgboost can support custom loss functions.
We can optimize every loss function, including logistic regression, weighted logistic regression, using exactly
We can optimize every loss function, including logistic regression and weighted logistic regression, using exactly
the same solver that takes ``$g_i$`` and ``$h_i$`` as input!
### Model Complexity
We have introduced the training step, but wait, there is one important thing, the ***regularization***!
We need to define the complexity of the tree ``$\Omega(f)$``. In order to do so, let us first refine the definition of the tree a tree ``$ f(x) $`` as
We need to define the complexity of the tree ``$\Omega(f)$``. In order to do so, let us first refine the definition of the tree ``$ f(x) $`` as
```math
f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} .
```
Here ``$ w $`` is the vector of scores on leaves, ``$ q $`` is a function assigning each data point to the corresponding leaf and``$ T $`` is the number of leaves.
Here ``$ w $`` is the vector of scores on leaves, ``$ q $`` is a function assigning each data point to the corresponding leaf, and``$ T $`` is the number of leaves.
In XGBoost, we define the complexity as
```math
@ -200,7 +200,7 @@ We could further compress the expression by defining ``$ G_j = \sum_{i\in I_j} g
\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T
```
In this equation ``$ w_j $`` are independent to each other, the form ``$ G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2 $`` is quadratic and the best ``$ w_j $`` for a given structure ``$q(x)$`` and the best objective reduction we can get is:
In this equation ``$ w_j $`` are independent with respect to each other, the form ``$ G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2 $`` is quadratic and the best ``$ w_j $`` for a given structure ``$q(x)$`` and the best objective reduction we can get is:
```math
w_j^\ast = -\frac{G_j}{H_j+\lambda}\\
@ -217,7 +217,7 @@ This score is like the impurity measure in a decision tree, except that it also
### Learn the tree structure
Now that we have a way to measure how good a tree is, ideally we would enumerate all possible trees and pick the best one.
In practice it is intractable, so we will try to optimize one level of the tree at a time.
In practice this is intractable, so we will try to optimize one level of the tree at a time.
Specifically we try to split a leaf into two leaves, and the score it gains is
```math
@ -230,7 +230,7 @@ models! By using the principles of supervised learning, we can naturally come up
For real valued data, we usually want to search for an optimal split. To efficiently do so, we place all the instances in sorted order, like the following picture.
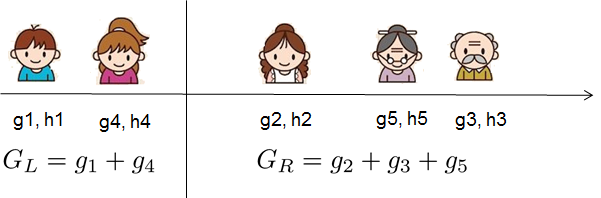
![Best split](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/split_find.png)
Then a left to right scan is sufficient to calculate the structure score of all possible split solutions, and we can find the best split efficiently.
A left to right scan is sufficient to calculate the structure score of all possible split solutions, and we can find the best split efficiently.
Final words on XGBoost
----------------------

50
doc/tutorials/aws_yarn.md
View File

@ -1,8 +1,8 @@
Distributed XGBoost YARN on AWS
===============================
This is a step-by-step tutorial on how to setup and run distributed [XGBoost](https://github.com/dmlc/xgboost)
on a AWS EC2 cluster. Distributed XGBoost runs on various platforms such as MPI, SGE and Hadoop YARN.
In this tutorial, we use YARN as an example since this is widely used solution for distributed computing.
on an AWS EC2 cluster. Distributed XGBoost runs on various platforms such as MPI, SGE and Hadoop YARN.
In this tutorial, we use YARN as an example since this is a widely used solution for distributed computing.
Prerequisite
------------
@ -38,21 +38,21 @@ Now we can launch a master machine of the cluster from EC2
```bash
./yarn-ec2 -k mykey -i mypem.pem launch xgboost
```
Wait a few mininutes till the master machine get up.
Wait a few mininutes till the master machine gets up.
After the master machine gets up, we can query the public DNS of the master machine using the following command.
```bash
./yarn-ec2 -k mykey -i mypem.pem get-master xgboost
```
It will show the public DNS of the master machine like ```ec2-xx-xx-xx.us-west-2.compute.amazonaws.com```
Now we can open the browser, and type(replace the DNS with the master DNS)
Now we can open the browser, and type (replace the DNS with the master DNS)
```
ec2-xx-xx-xx.us-west-2.compute.amazonaws.com:8088
```
This will show the job tracker of the YARN cluster. Note that we may wait a few minutes before the master finishes bootstrapping and starts the
This will show the job tracker of the YARN cluster. Note that we may have to wait a few minutes before the master finishes bootstrapping and starts the
job tracker.
After master machine gets up, we can freely add more slave machines to the cluster.
After the master machine gets up, we can freely add more slave machines to the cluster.
The following command add m3.xlarge instances to the cluster.
```bash
./yarn-ec2 -k mykey -i mypem.pem -t m3.xlarge -s 2 addslave xgboost
@ -61,17 +61,17 @@ We can also choose to add two spot instances
```bash
./yarn-ec2 -k mykey -i mypem.pem -t m3.xlarge -s 2 addspot xgboost
```
The slave machines will startup, bootstrap and report to the master.
You can check if the slave machines are connected by clicking on Nodes link on the job tracker.
Or simply type the following URL(replace DNS ith the master DNS)
The slave machines will start up, bootstrap and report to the master.
You can check if the slave machines are connected by clicking on the Nodes link on the job tracker.
Or simply type the following URL (replace DNS ith the master DNS)
```
ec2-xx-xx-xx.us-west-2.compute.amazonaws.com:8088/cluster/nodes
```
One thing we should note is that not all the links in the job tracker works.
This is due to that many of them uses the private ip of AWS, which can only be accessed by EC2.
One thing we should note is that not all the links in the job tracker work.
This is due to that many of them use the private IP of AWS, which can only be accessed by EC2.
We can use ssh proxy to access these packages.
Now that we have setup a cluster with one master and two slaves. We are ready to run the experiment.
Now that we have set up a cluster with one master and two slaves, we are ready to run the experiment.
Build XGBoost with S3
@ -92,7 +92,7 @@ cp make/config.mk config.mk
echo "USE_S3=1" >> config.mk
make -j4
```
Now we have built the XGBoost with S3 support. You can also enable HDFS support if you plan to store data on HDFS, by turnning on ```USE_HDFS``` option.
Now we have built the XGBoost with S3 support. You can also enable HDFS support if you plan to store data on HDFS by turning on ```USE_HDFS``` option.
XGBoost also relies on the environment variable to access S3, so you will need to add the following two lines to `~/.bashrc` (replacing the strings with the correct ones)
on the master machine as well.
@ -107,7 +107,7 @@ Host the Data on S3
-------------------
In this example, we will copy the example dataset in xgboost to the S3 bucket as input.
In normal usecases, the dataset is usually created from existing distributed processing pipeline.
We can use [s3cmd](http://s3tools.org/s3cmd) to copy the data into mybucket(replace ${BUCKET} with the real bucket name).
We can use [s3cmd](http://s3tools.org/s3cmd) to copy the data into mybucket (replace ${BUCKET} with the real bucket name).
```bash
cd xgboost
@ -120,7 +120,7 @@ Submit the Jobs
Now everything is ready, we can submit the xgboost distributed job to the YARN cluster.
We will use the [dmlc-submit](https://github.com/dmlc/dmlc-core/tree/master/tracker) script to submit the job.
Now we can run the following script in the distributed training folder(replace ${BUCKET} with the real bucket name)
Now we can run the following script in the distributed training folder (replace ${BUCKET} with the real bucket name)
```bash
cd xgboost/demo/distributed-training
# Use dmlc-submit to submit the job.
@ -134,7 +134,7 @@ All the configurations such as ```data``` and ```model_dir``` can also be direct
Note that we only specified the folder path to the file, instead of the file name.
XGBoost will read in all the files in that folder as the training and evaluation data.
In this command, we are using two workers, each worker uses two running thread.
In this command, we are using two workers, and each worker uses two running threads.
XGBoost can benefit from using multiple cores in each worker.
A common choice of working cores can range from 4 to 8.
The trained model will be saved into the specified model folder. You can browse the model folder.
@ -157,28 +157,28 @@ Application application_1456461717456_0015 finished with state FINISHED at 14564
Analyze the Model
-----------------
After the model is trained, we can analyse the learnt model and use it for future prediction task.
XGBoost is a portable framework, the model in all platforms are ***exchangeable***.
After the model is trained, we can analyse the learnt model and use it for future prediction tasks.
XGBoost is a portable framework, meaning the models in all platforms are ***exchangeable***.
This means we can load the trained model in python/R/Julia and take benefit of data science pipelines
in these languages to do model analysis and prediction.
For example, you can use [this ipython notebook](https://github.com/dmlc/xgboost/tree/master/demo/distributed-training/plot_model.ipynb)
For example, you can use [this IPython notebook](https://github.com/dmlc/xgboost/tree/master/demo/distributed-training/plot_model.ipynb)
to plot feature importance and visualize the learnt model.
Trouble Shooting
Troubleshooting
----------------
When you encountered a problem, the best way might be use the following command
to get logs of stdout and stderr of the containers, to check what causes the problem.
If you encounter a problem, the best way might be to use the following command
to get logs of stdout and stderr of the containers and check what causes the problem.
```
yarn logs -applicationId yourAppId
```
Future Directions
-----------------
You have learnt to use distributed XGBoost on YARN in this tutorial.
XGBoost is portable and scalable framework for gradient boosting.
You can checkout more examples and resources in the [resources page](https://github.com/dmlc/xgboost/blob/master/demo/README.md).
You have learned to use distributed XGBoost on YARN in this tutorial.
XGBoost is a portable and scalable framework for gradient boosting.
You can check out more examples and resources in the [resources page](https://github.com/dmlc/xgboost/blob/master/demo/README.md).
The project goal is to make the best scalable machine learning solution available to all platforms.
The API is designed to be able to portable, and the same code can also run on other platforms such as MPI and SGE.

16
doc/tutorials/dart.md
View File

@ -1,9 +1,9 @@
DART booster
============
[XGBoost](https://github.com/dmlc/xgboost)) mostly combines a huge number of regression trees with small learning rate.
In this situation, trees added early are significance and trees added late are unimportant.
[XGBoost](https://github.com/dmlc/xgboost)) mostly combines a huge number of regression trees with a small learning rate.
In this situation, trees added early are significant and trees added late are unimportant.
Rasmi et.al proposed a new method to add dropout techniques from deep neural nets community to boosted trees, and reported better results in some situations.
Rasmi et al. proposed a new method to add dropout techniques from the deep neural net community to boosted trees, and reported better results in some situations.
This is a instruction of new tree booster `dart`.
@ -16,15 +16,15 @@ Features
- Drop trees in order to solve the over-fitting.
- Trivial trees (to correct trivial errors) may be prevented.
Because the randomness introduced in the training, expect the following few difference.
- Training can be slower than `gbtree` because the random dropout prevents usage of prediction buffer.
Because of the randomness introduced in the training, expect the following few differences:
- Training can be slower than `gbtree` because the random dropout prevents usage of the prediction buffer.
- The early stop might not be stable, due to the randomness.
How it works
------------
- In ``$ m $``th training round, suppose ``$ k $`` trees are selected drop.
- Let ``$ D = \sum_{i \in \mathbf{K}} F_i $`` be leaf scores of dropped trees and ``$ F_m = \eta \tilde{F}_m $`` be leaf scores of a new tree.
- The objective function is following:
- In ``$ m $``th training round, suppose ``$ k $`` trees are selected to be dropped.
- Let ``$ D = \sum_{i \in \mathbf{K}} F_i $`` be the leaf scores of dropped trees and ``$ F_m = \eta \tilde{F}_m $`` be the leaf scores of a new tree.
- The objective function is as follows:
```math
\mathrm{Obj}
= \sum_{j=1}^n L \left( y_j, \hat{y}_j^{m-1} - D_j + \tilde{F}_m \right)

2
doc/tutorials/index.md
View File

@ -1,7 +1,7 @@
# XGBoost Tutorials
This section contains official tutorials inside XGBoost package.
See [Awesome XGBoost](https://github.com/dmlc/xgboost/tree/master/demo) for links to mores resources.
See [Awesome XGBoost](https://github.com/dmlc/xgboost/tree/master/demo) for links to more resources.
## Contents
- [Introduction to Boosted Trees](../model.md)

10
doc/tutorials/monotonic.md
View File

@ -1,7 +1,7 @@
Monotonic Constraints
=====================
It is often the case ina modeling problems or project that the functional form of an acceptable model is constrained in some way. This may happen due to business considerations, or because of the type of scientific question being investigated. In some cases, where there is a very strong prior belief that the true relationship has some quality, constraints can be used to improve the predictive performance of the model.
It is often the case in a modeling problem or project that the functional form of an acceptable model is constrained in some way. This may happen due to business considerations, or because of the type of scientific question being investigated. In some cases, where there is a very strong prior belief that the true relationship has some quality, constraints can be used to improve the predictive performance of the model.
A common type of constraint in this situation is that certain features bear a *monotonic* relationship to the predicted response:
@ -9,13 +9,13 @@ A common type of constraint in this situation is that certain features bear a *m
f(x_1, x_2, \ldots, x, \ldots, x_{n-1}, x_n) \leq f(x_1, x_2, \ldots, x', \ldots, x_{n-1}, x_n)
```
whenever ``$ x \leq x' $``, an *increasing constraint*; or
whenever ``$ x \leq x' $`` is an *increasing constraint*; or
```math
f(x_1, x_2, \ldots, x, \ldots, x_{n-1}, x_n) \geq f(x_1, x_2, \ldots, x', \ldots, x_{n-1}, x_n)
```
whenever ``$ x \leq x' $``, a *decreasing constraint*.
whenever ``$ x \leq x' $`` is a *decreasing constraint*.
XGBoost has the ability to enforce monotonicity constraints on any features used in a boosted model.
@ -38,7 +38,7 @@ Let's fit a boosted tree model to this data without imposing any monotonic const
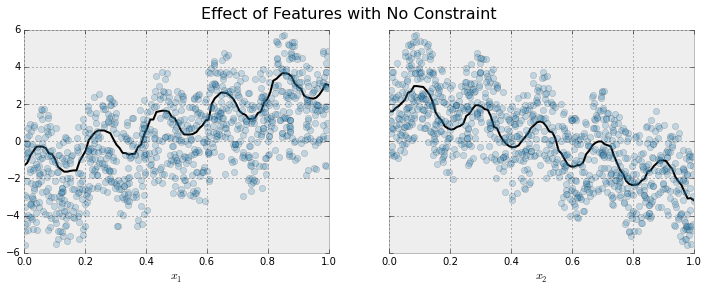
![Fit of Model with No Constraint](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/monotonic/two.feature.no.constraint.png)
The black curve shows the trend inferred from the model for each feature. To make these plots the distinguished feature ``$x_i$`` is fed to the model over a one dimensional grid of values, while all the other features (in this case only one other feature) are set to their average values. We see that the model does a good job of capturing the general trend with the oscillatory wave superimposed.
The black curve shows the trend inferred from the model for each feature. To make these plots the distinguished feature ``$x_i$`` is fed to the model over a one-dimensional grid of values, while all the other features (in this case only one other feature) are set to their average values. We see that the model does a good job of capturing the general trend with the oscillatory wave superimposed.
Here is the same model, but fit with monotonicity constraints
@ -70,7 +70,7 @@ model_with_constraints = xgb.train(params_constrained, dtrain,
early_stopping_rounds = 10)
```
In this example the training data ```X``` has two columns, and by unsing the parameter value ```(1,-1)``` we are telling XGBoost to impose an increaseing constraint on the first predictor and a decreasing constraint on the second.
In this example the training data ```X``` has two columns, and by using the parameter values ```(1,-1)``` we are telling XGBoost to impose an increasing constraint on the first predictor and a decreasing constraint on the second.
Some other examples: