Move model doc images to web-data (#1397)

doc/model.md

@@ -51,7 +51,7 @@ This sounds a bit abstract, so let us consider the following problem in the foll
 on the upper left corner of the image.
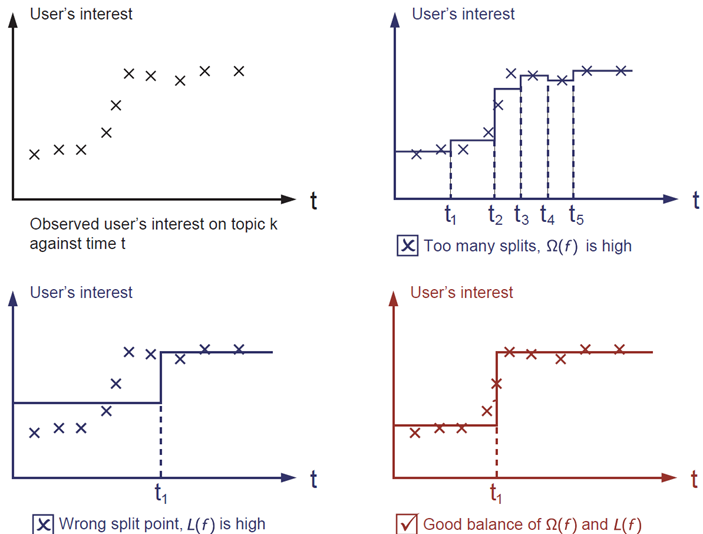
 Which solution among the three do you think is the best fit?
 
-![Step function](img/step_fit.png)
+![Step function](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/step_fit.png)
 
 The answer is already marked as red. Please think if it is reasonable to you visually. The general principle is we want a ***simple*** and ***predictive*** model.
 The tradeoff between the two is also referred as bias-variance tradeoff in machine learning.
@@ -70,7 +70,7 @@ To begin with, let us first learn about the ***model*** of xgboost: tree ensembl
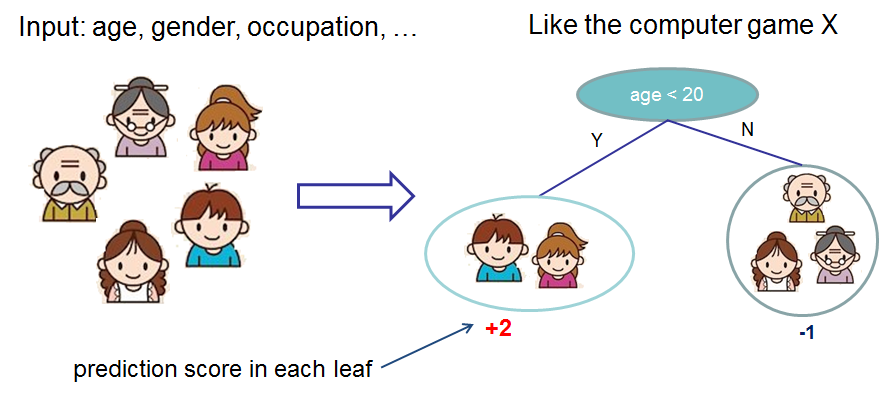
 The tree ensemble model is a set of classification and regression trees (CART). Here's a simple example of a CART
 that classifies whether someone will like computer games.
 
-![CART](img/cart.png)
+![CART](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/cart.png)
 
 We classify the members of a family into different leaves, and assign them the score on corresponding leaf.
 A CART is a bit different from decision trees, where the leaf only contains decision values. In CART, a real score
@@ -80,7 +80,7 @@ This also makes the unified optimization step easier, as we will see in later pa
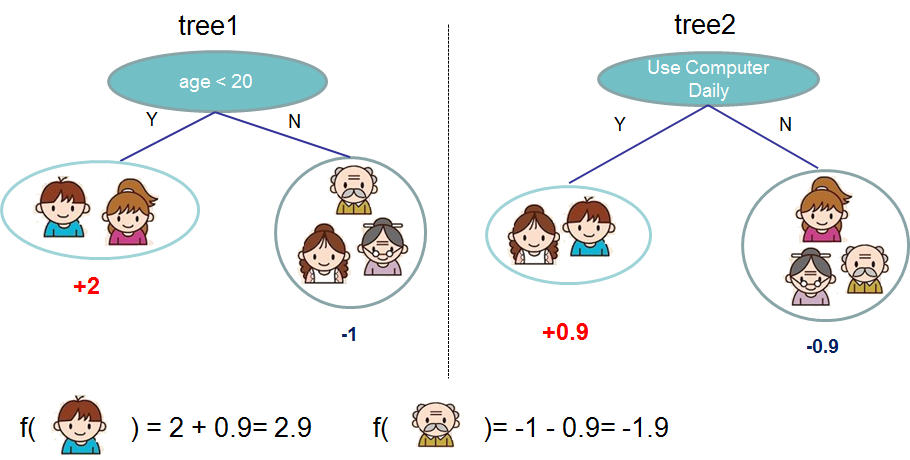
 Usually, a single tree is not strong enough to be used in practice. What is actually used is the so-called
 tree ensemble model, that sums the prediction of multiple trees together.
 
-![TwoCART](img/twocart.png)
+![TwoCART](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/twocart.png)
 
 Here is an example of tree ensemble of two trees. The prediction scores of each individual tree are summed up to get the final score.
 If you look at the example, an important fact is that the two trees try to *complement* each other.
@@ -208,7 +208,7 @@ Obj^\ast = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T
 ```
 The last equation measures ***how good*** a tree structure ``$q(x)$`` is.
 
-![Structure Score](img/struct_score.png)
+![Structure Score](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/struct_score.png)
 
 If all this sounds a bit complicated, let's take a look at the picture, and see how the scores can be calculated.
 Basically, for a given tree structure, we push the statistics ``$g_i$`` and ``$h_i$`` to the leaves they belong to,
@@ -228,7 +228,7 @@ We can see an important fact here: if the gain is smaller than ``$\gamma$``, we
 models! By using the principles of supervised learning, we can naturally come up with the reason these techniques work :)
 
 For real valued data, we usually want to search for an optimal split. To efficiently do so, we place all the instances in sorted order, like the following picture.
-![Best split](img/split_find.png)
+![Best split](https://raw.githubusercontent.com/dmlc/web-data/master/xgboost/model/split_find.png)
 
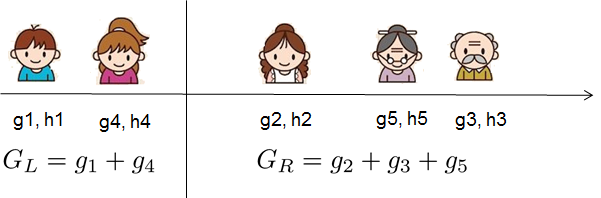
 Then a left to right scan is sufficient to calculate the structure score of all possible split solutions, and we can find the best split efficiently.